For sound generation in music applications often a precise sine wave is required. One of the best known methods to do this is an approximation performed by the so called DDS:

Function of DDS

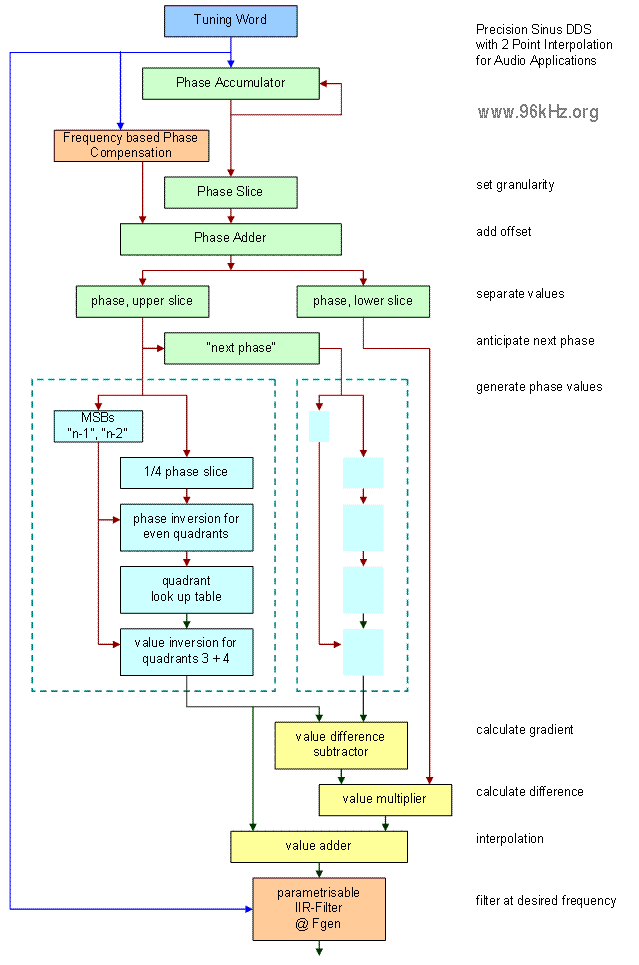
The sine wave is stored in a table and read with an address counter derived from an accumulator which represents the phase. These tables can easily be generated with Excel. Mostly 90 degrees of the wave are stored only. The values for other angles are than derived by angle mapping and point inversion. Here we will discuss two possibilities to store the values:

Definition of the phase

Most people use the borders of the focused region when defining the phase such as 0.0, 1.0, 2.0, 3.0, ... (n/4)-1 und repeat the curve backwards starting from the point n/4. This leads to 32 points in this case with the coordinates [0,1,2,3,4,5,6,7] and [8,7,6,5,4,3,2,1] which are repeated again with inverted sign for angles beyond 180 degrees. This means the fundamental element starts at the angles 0, 90, 180 and 270 and does not include the last point of the area not to get this point twice. So the phases are p = 0, 1/n, 2/n ... (n-1)/n. It is important to mention that the division required to find the relative angle has to be performed with "n" and not with "n-1", what some people do. The dots generated this way, first cover a full period with 17 values / 9 values  0…180° = π. There are two slightly different quarters which are not symmetrical to each other. Another bit is required to represent the phase vector because of the (0…7) / (1…8) issue.

From the point of the ease of calculation and symmetry purposes it seems more appropriate to focus the mid of the ranges defined by the digital virtual phase 0 ... n-1. This leads in (this case) to 8 points in each quarter which are totally identical. The digital value 0 addressing the first dot represents it's region by the average value of the region and the value 7 does the same for the region between point 7 and point 8. To get the right value, a correction of Phase/n has to added to the phase vector. Thus the phase values are p = 0,5 , 1,5/n, 2,5/n ... (n-0,5)/n. The vector has the same size for all quarters and saves one bit.

Definition of the amplitude

Depending on the integer range used for the scale of the sine wave, it is necessary to use one bit more for just representing the maximum value, especially with small number of points. With the unsymmetrical representation, one should think about if it is really necessary to use the full "2 by n" range. Sometimes it is better to limit the maximum value, for example to maintain symmetry for a certain value. Especially with method 1, there is a true zero point, and the most negative value e.g. "-128" at 8 bits can be left away.

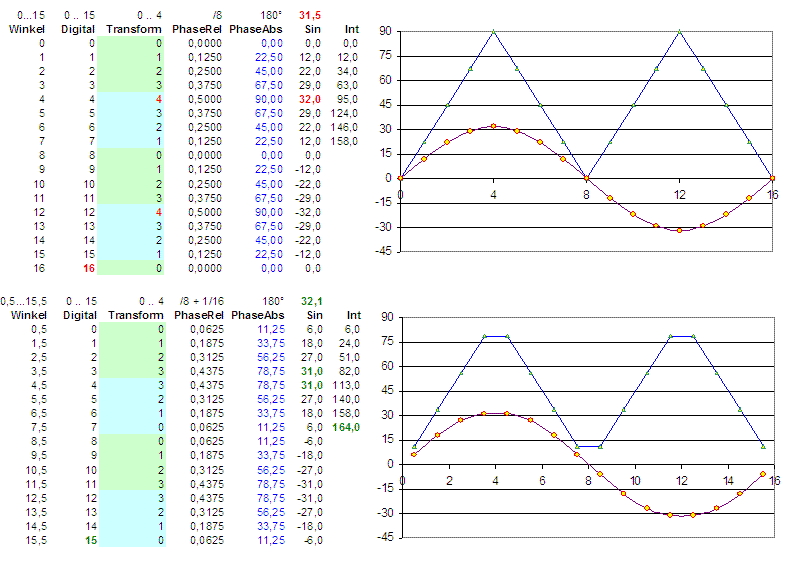
Graphical representation of the two possible declarations starting with the angle as a float value in between 0 ... X ... 16, and it's digital "code" from 0 ... 15, the focused sector of the sine wave (please have a look at the special point 4), the relative phase related to the sector origin, the absolute phase in between 360 degrees and the resulting sine waves. The added values in the right row (int) give an impression of the  integral = energy of the curve. The curves represent the 4 used points. The blue curve represents the angle from 0 ... 90 degrees.

Analytical calculation of sine values

This is a "sine wave" I found in my early days in the 80tees doing experiments with Commodore VC20 / VC64 and Assembler. Unlike in Basic, there was no sin(x) available.

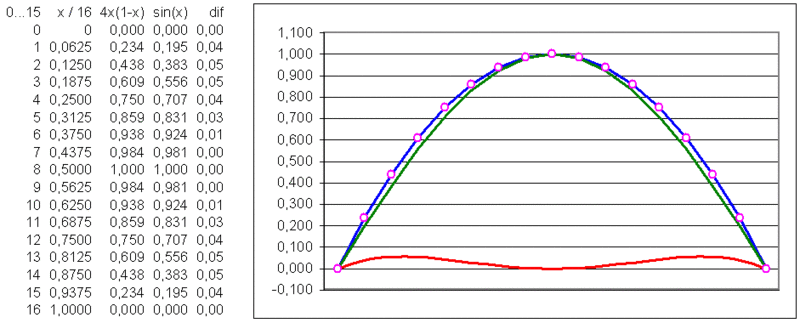
The equation is easy and has only 6% of error.

Y = x * (1 - x) / 4

Interestingly it sounds more musical than the boring sine wave :-)

optimized equation for microcontrollers

This sine wave equation meets the requirements of easy and quick processing in microcontrollers especially when programmed in assembler language.

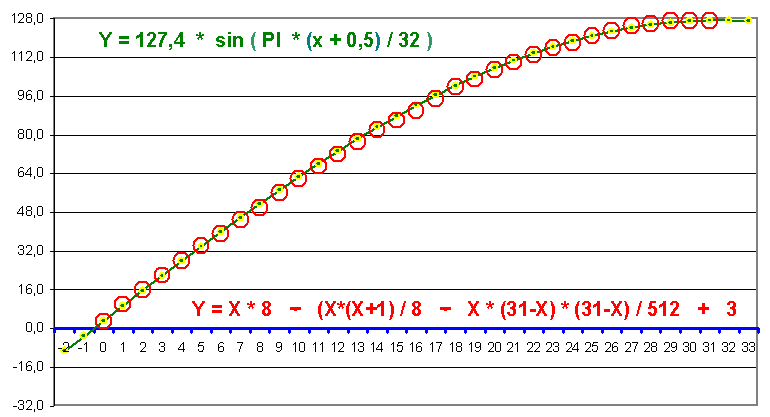
It uses fundamental binary operations only, but though produces a pretty precise sine wave with only 1 digit error in maximum. Digital systems can process it easily by using shift operations for multiplication and division.

Read about some examples and issues with DDS