For sound generation in music applications, often a precise sine wave is required. The best known method to do this directly in the digital domain is to use an approximation of the sine wave and continuously repeat it - performed by the so called DDS:

Function of DDS

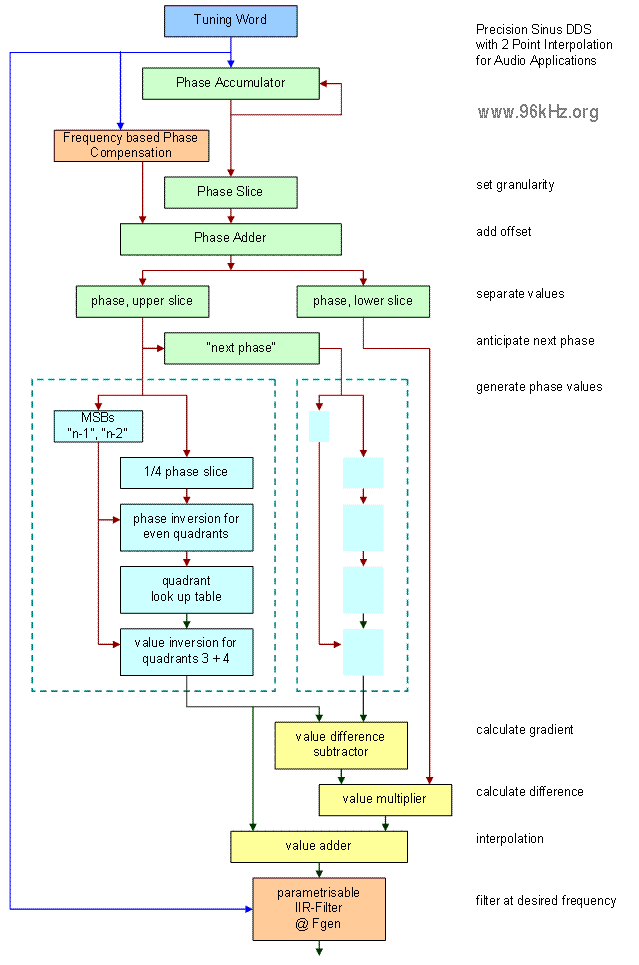
The sine wave is stored in a table and read with an address counter derived from an accumulator which represents the phase. These tables can easily be generated with Excel. 90 degrees of the wave are stored and the values for other angles are than derived by angle mapping and point inversion. In the above example, interpolation is used by simultaneously calculation two points for one point of time and using the debris after cutting the phase vector (in order to obtain the address) as a parameter for a linear equation.

The limit of the phase vector

Because of the fact that even with interpolation the phase vector is limited in size and also the frequency does no 100% fit into the length of the table, some points are missed or repeated during continuous stepping though the table leading to a shifted part of the sine wave and thus to a false representation. The phase errors are later filtered by the anti aliasing filter, but cannot be eliminated perfectly.

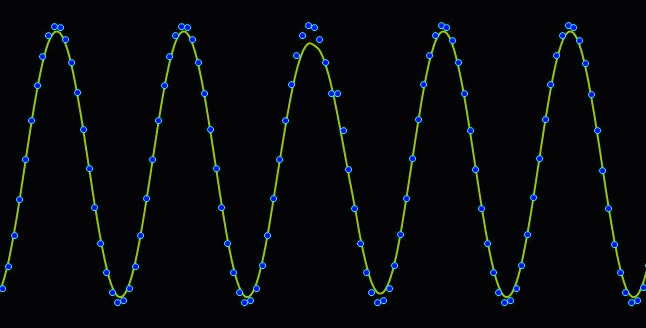
 Comparing the resulting value with the theoretical ideal value shows a difference which is again a sine curve over a given period. The following image gives an example:

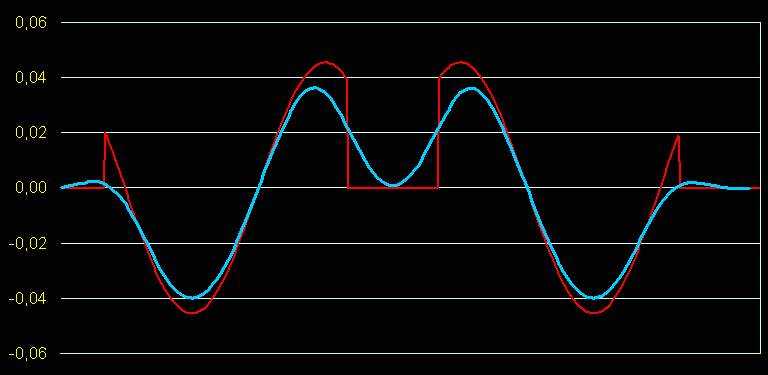
The red curve shows the absolute difference between the ideal theoretical function sin(x) and the used function sin (int (k * x) /k), which represents the integer rounding of the phase vector. The effect is already visually very pronounced. The resulting wave introduces noise and distortion into the sound, which is partially reduced by the anti-aliasing filter at the output, represented by the cyan curve. The phase jumps result in more or less regularly recurring wave packets, some with very low frequencies, which hardly benefit from the filtering and therefore produce clearly audible noise and distortion in the final signal.

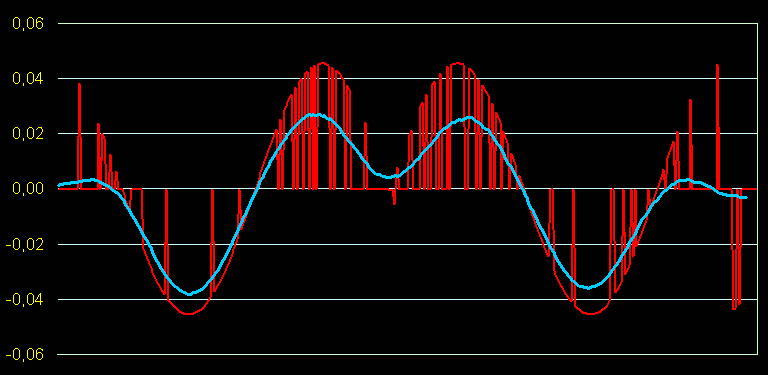
The problem can be significantly reduced by phase dithering methods. Adding additional noise causes significant interference at first sight, but leads to a few wrong signal after filtering, because the error noise is shifted to higher frequencies, which are better filtered away. In particular, the previously clearly audible low-frequency components of the interference are greatly reduced.

Design Recommendation

To obtain a sine wave well suited for audio applications, the DDS sampling frequency should be at least 100 times higher than the highest frequency to be reproduced. For the future sound standard for audio systems with 96kHz, this means that frequencies up to about 1kHz can be reproduced almost perfectly. At higher frequencies, artifacts must increasingly be accepted, or more complex filtering is required. This problem applies even more to all attempts to generate non-sinusoidal waves whose amplitude values are stored in a table, since these can contain particularly high harmonics.

See also:

Sine waves with DDS

Wave Synthesis in PLDs