| 96 kHz.org |
| Advanced Audio Recording |
Comparison of 48kHz and 96kHz sample frequency for audio recording In recent years 96kHz sampling frequency was recommended for modern audio recording. This article shows some technical background, why this is the case. Please also read the article: Do we need 96kHz ?
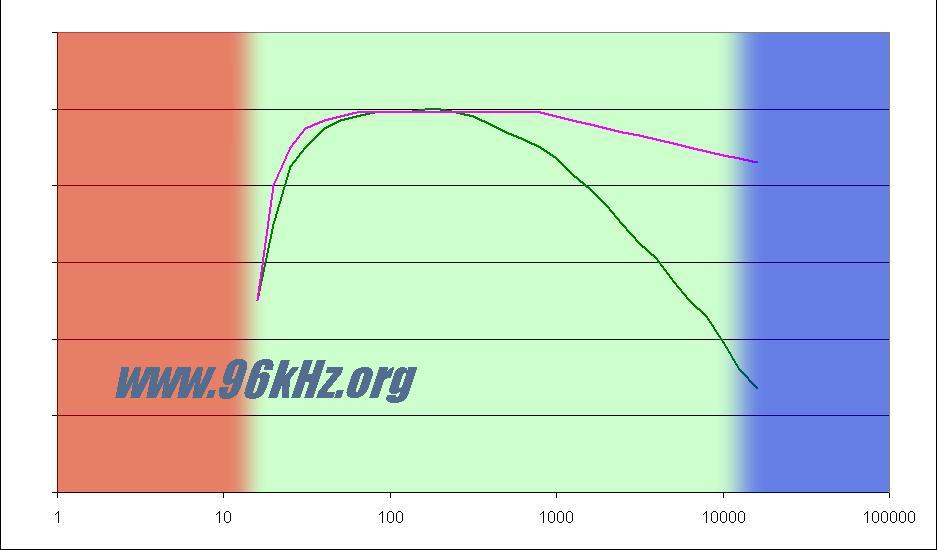
The advantage of higher sampling frequencies From the theory the current 48kHz frequency seems to be sufficient since it can represent up to 24kHz which is the half of the sample rate and defines the so called Nyquist's frequency. Using an appropriate reconstruction filter, all frequencies below this border might be correctly restored. Practically this required an ideal anti aliasing filter which does not exist and cannot be constructed neither in analog nor in digital domains. This leads to the conclusion that some headroom is necessary to reduce the amount of frequencies beyond Nyquist's to omit mirror frequencies. The subsequent image shows natural frequencies from 10Hz up to 100kHz ("whales to bats") and the audible range which can be recognized by most humans shown as an average sensitivity curve for medium loudness. Furthermore a typical mixing curve of music is shown too:
It quickly becomes evident, that there is not much space in between a reasonable band limit of e.g. 15kHz and the Nyquist's frequency when using 48kHz sample rate. Therefore a well defined filter has to be selected offering a good compromise between ripple and band stop capabilities. On the other hand, the loudness of the upper bands is usually significantly lower than in the lower bands thus a trade off between a correct frequency representation and linearity seems possible.
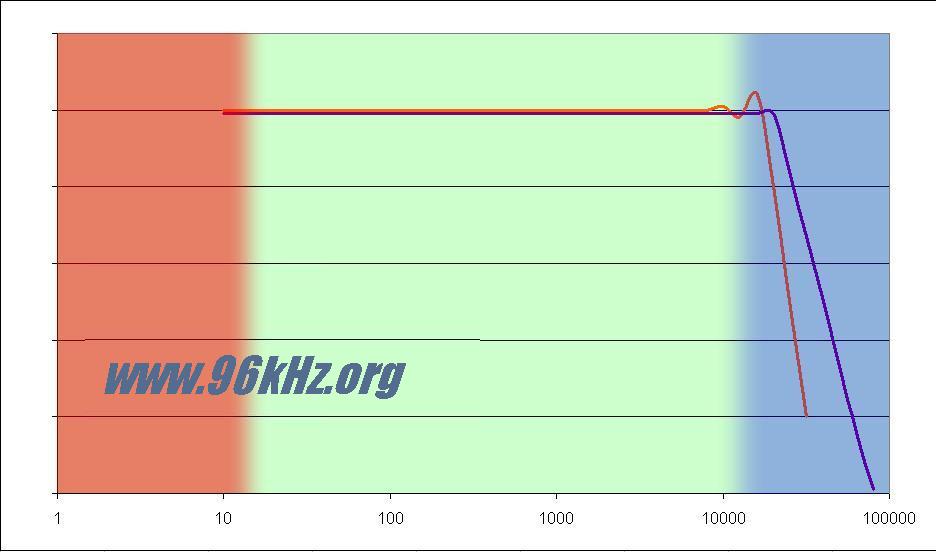
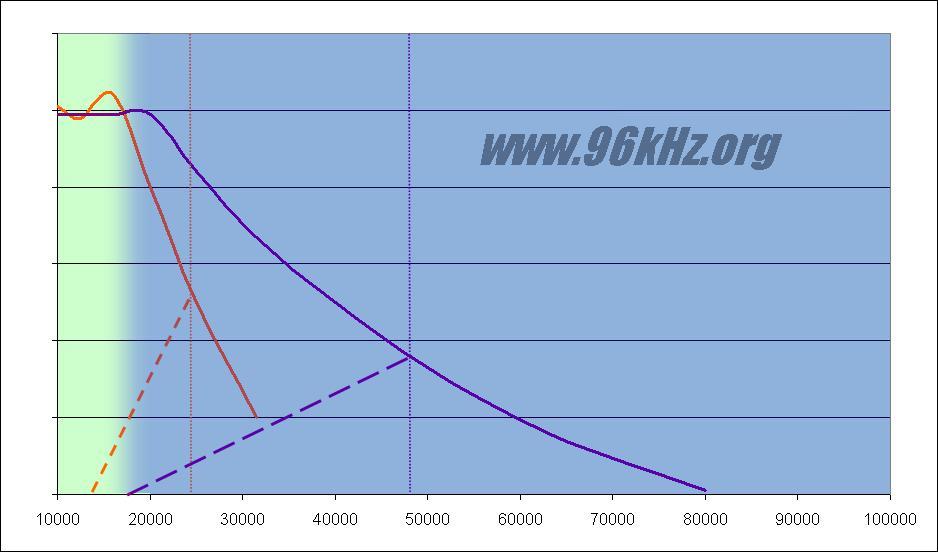
The orange curve in the following image shows such a filter having low ripple and is steep enough to meet a 48kHz sampling frequency. Though using 96kHz makes things much easier. A more flat and therefore nearly ripple free filter can be used, because the headroom is much bigger. The filter just has to make sure, that there are no (or nearly no) frequencies beyond 48kHz which is the Nyquist's frequency when using 96kHz. The subsequent image shows the introduced mirror frequencies for both cases in an enlarged view with linear scale:
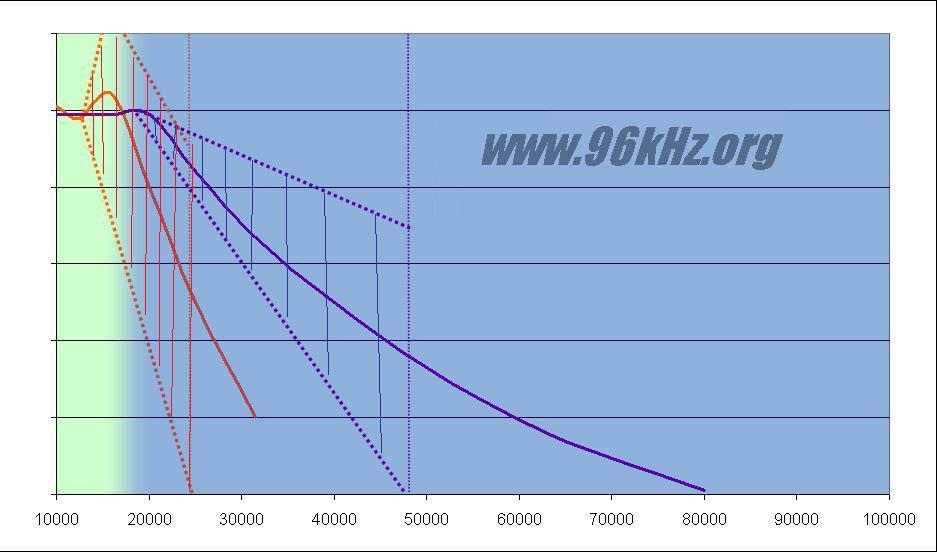
Frequencies beyond Nyquist's are flipped over and add to the real signals causing aliasing. Of course there will be a debris also with 96kHz but it will do no harm even with such a flat filter like shown in the graphics, since the caused mirror frequencies will stay in the non audible range and disappear from the signal during reconstruction. The last image gives an impression of the frequency range which is affected by the aliasing frequencies:
The aliasing frequencies cause a deformation of the filter curve depending on their individual amplitude and phase, so the region close to the Nyquist's frequency becomes more and more false.
Conclusion and
Summary
|
| © 2003 J.S. |