A triple loop Waveguide-Oscillator for String-Sound-Synthesis

a 3-stage wave guide oscillator in VHDL
	DSP Module	A VHDL-implementation of my multi stage delay oscillator is presented here. It works with a similar method as known from the Karplus-Strong-Algorithm and formerly had been implemented in my Chameleon using C-language for DSP56301, see the KSA-page. 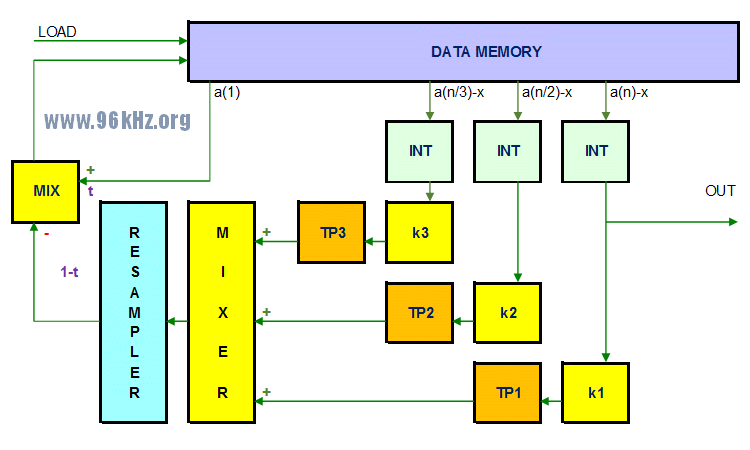The design works with 48kHz sample frequency and almost 12,288 MHz FPGA clock frequency offering 256-times oversampling. 3 feedback loops are used to drive harmonics into the circuit, making the sound more realistic and let it come closer to the intended string instruments. The feedbacks are scaled adequately and added to the existing mix so that the overall energy disappears in a slow and controlled way. Here MIX1 block works as a low pass filter taking the most recent sample(s) into account. The advantage in comparison to known designs with only one loop is the more realistic behaviour of the harmonics that way that multiples of the fundamental frequency are driven into the system too thus maintaining or even emphasizing these harmonics as it also takes place with real strings. The very special issue about that is that one can also tune the address vectors and control the ram access that way that the resulting period is a little bit different than e.g. a 1/3 of the string lengths which even more represents the reality in a better way since strings with a real lenghts do not totally adhere the diffential equations which describe infinite wires without any weight. By using equalizers (TP1 ... TP3) - possible low pass filters- the harmonics can be furtherly controlled. At least one IIR ("MIX") should be present to limit high frequencies and upcoming alias frequencies. In the images below one can see the behaviour of the waves when using the feedback of the third harmonic 1) not at all, 2) slightly a bit and 3) in an excessive way. The screenshots have been taken from my VGA-oscilloscope and copied together for all three cases in sequence showing 12 points of time each. Examples: 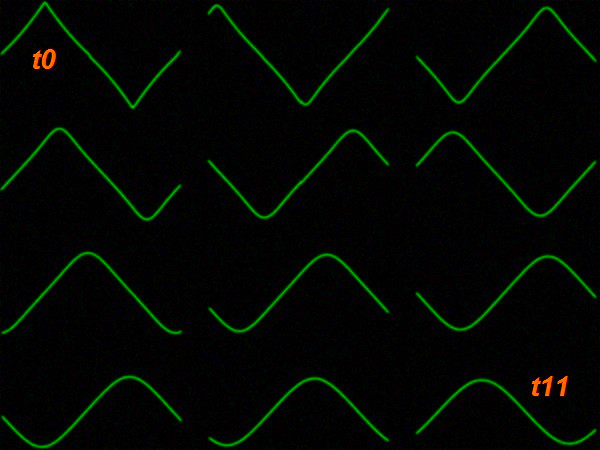Without the feedback the harmonics (introduced by a triangle) simply vanish so that the wave becomes a sine wave. This is not really realistic because the nature of the string is to reintroduce harmonics. A slight feedback of the third makes sure this works.The wave is always "living" and has harmonics with an automatically balanced level. 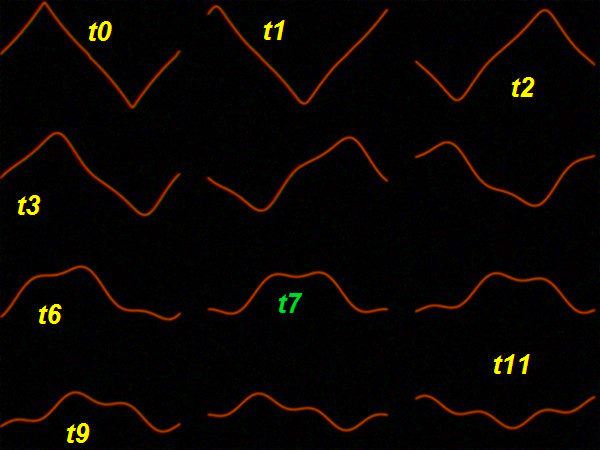Strong feedbacks will cause a rapid redistribution of the energy in the string into the third ending up that way that almost flattended waves (partly similar to squares) occur, depending on the phase of the harmonic (T6, T7, T8). The sound if similar to an electric distorted guitar. Attention: It has to be mentined that this approach is partly overlapping with the Patent of Karplus and Strong. In order not to violate this, a trick might be used: One undersamples the outgoing data stream slightly and truncates the delay appropriately so that the resulting feedback pitches correspond. This practically creates a de facto band limiter too if done well without using an explicit lowpass like given in the patent. However care should be taken for the amount of harmonics introduced into the signal then. Extensions: I experimented with more than 3 stages but found that too many harmonics may cause rubish if not set perfectly in terms of reloop steps and interpolation. One must not forget that after each loop some harmonics of the harmonics will be introduced. Finally I suggest to go with mainly H3 and H5. See the VHDL here: wgosc3.zip See the former version in C here: waveguide oscillator
	Xilinx Spartan II FPGA

	48 kHz Audio DSP