| 96 kHz.org |
| Advanced Audio Recording |
|
Window Equations This page describes some window functions for smoothing purposes during audio processing and mixing which can easily be calculated. They are especially suitable for smoothing audio data which is processed in real time when filter parameters have to change too. Basically the windows use squares and cubics of a function obtained by integrating a parabolic curve.
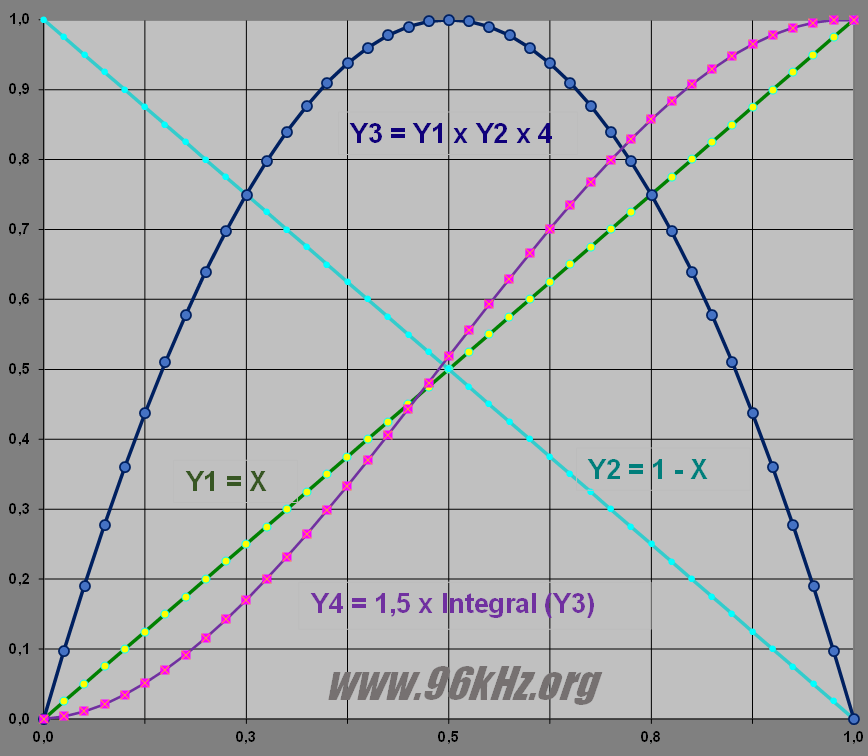
Smoothed fading Let's take a simple cross fade of y = A * k + B * (1-k). It is clear that the equation Y = x * (1-x) will create a smoothed parabolic behavior in between 0 ... 1 with zeros at it's ends. To use is it should be scaled by ratio 4. The integral equation of this "x - x2" would be x*x/2 + x*x*x/3. With a scale factor of 6 it leads to the S1-curve which is a smoothed curve softly fading from 0 ... 1 for y.
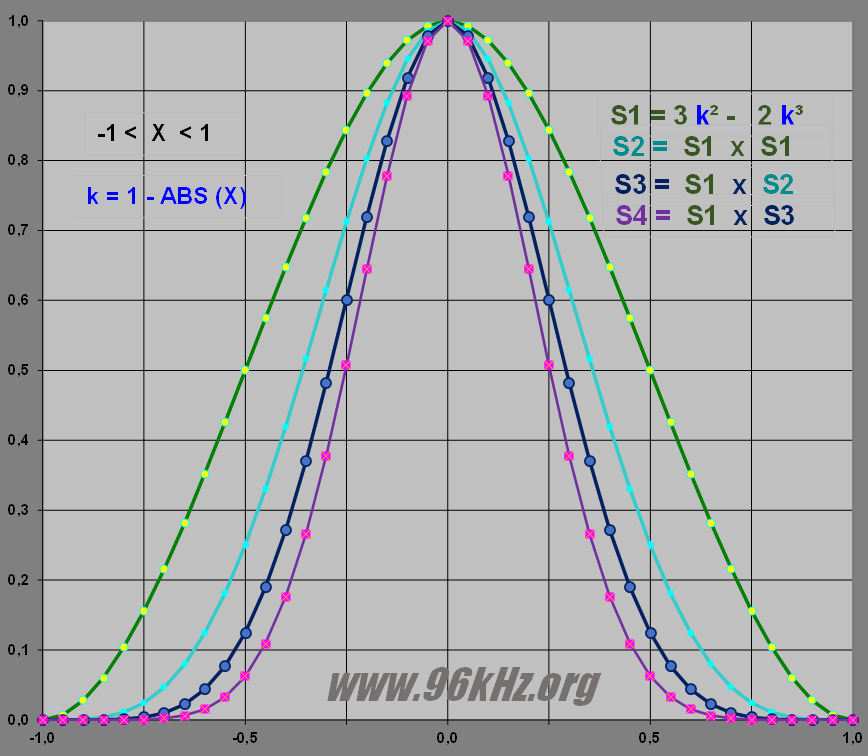
Now let's scale and move the window into the middle and mirror the coordinates for x leading to "k".
To make use of a given number of samples to be smoothed the range has to be changed from -1 to +1 (representation for X) or 0 ... 1 like assume for parameter "k" in the diagram. More steeper functions are obtained by the square and e.g. the cubic of the S1-function.
Usage The S1 function is best used for cross fading two independent audio channels. It also can be used to synthesize basic sinodial waves. For FFT-processing they appear similar to the "von-Hann-window". It can even emulate the Bessel behavior up to the values below 3.85 when scaled to this region. The S2/S3-functions performed nice as replacements for modified Kaiser windows of lower orders 3..5. The S2 window performed nice as a replacement for a selective window when scale to 0,9 and raised by 0,1, like Hamming's window. The selective S4 might be used together with spectral filter applications. The simple X2-function can be used to fade in between two audio signals maintaing their statistical energy and loudness.
Conclusion and Summary Simple equations can be used to smooth sampling data to process audio with low DSP usage.
|
| © 2002 - Jürgen Schuhmacher |