For sound generation in music synthesizers and industrial systems, often a precise sine wave is required. There are several methods to do this like the table based approximation used with classical DDS: The sine wave is stored in a RAM/ROM and directly read with an address counter derived from an accumulator representing the phase. These tables can easily be generated by e.g. an Excel sheet of MATLAB. Often only 90 degrees of the sine wave are stored and the values for other angles are derived by angle mapping and eventual level inversion. Here we can find two possibilities to store the values:

Representation of the phase vector in DDS

Most people use the borders of the focused region when defining the phase such as 0.0, 1.0, 2.0, 3.0, ... (n/4)-1 und repeat the curve backwards starting from the point n/4. This leads to 32 points in this case with the coordinates [0,1,2,3,4,5,6,7] and [8,7,6,5,4,3,2,1] which are repeated aging with inverted sign for angles beyond 180 degrees. This means the fundamental element starts at the angles 0, 90, 180 and 270 and does not include the last point of the area not to get this point twice. So the phases are p = 0, 1/n, 2/n ... (n-1)/n. It is important to mention that the division required to find the relative angle has to be performed with "n" and not with "n-1", what some people do. The dots generated this way, first cover a full period with 17 values / 9 values  0…180° = π. There are two slightly different quarters which are not symmetrical to each other. Another bit is required to represent the phase vector because of the (0…7) / (1…8) issue.

From the point of the ease of calculation and symmetry purposes it seems more appropriate to focus the mid of the ranges defined by the digital virtual phase 0 ... n-1. This leads in (this case) to 8 points in each quarter which are totally identical. The digital value 0 addressing the first dot represents it's region by the average value of the region and the value 7 does the same for the region between point 7 and point 8. To get the right value, a correction of Phase/n has to added to the phase vector. Thus the phase values are p = 0,5 , 1,5/n, 2,5/n ... (n-0,5)/n. The vector has the same size for all quarters and saves one bit.

Representation of the amplitude

Depending on the integer range used for the scale of the sine wave, it is necessary to use one bit more for just representing the maximum value, especially with small number of points. With the unsymmetrical representation, one should think about if it is really necessary to use the full "2 by n" range. Sometimes it is better to limit the maximum value, for example to maintain symmetry for a certain value. Especially with method 1, there is a true zero point, and the most negative value e.g. "-128" at 8 bits can be left away.

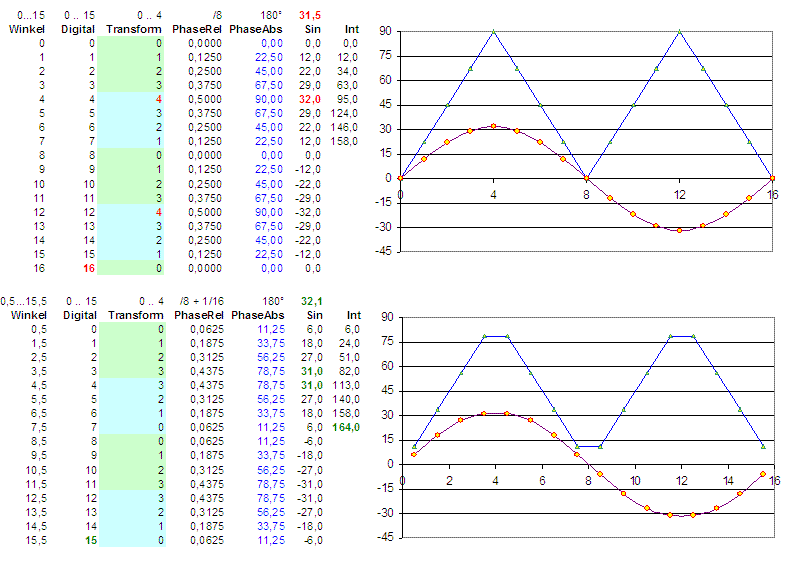
Graphical representation of the two possible declarations starting with the angle as a float value in between 0 ... X ... 16, and it's digital "code" from 0 ... 15, the focused sector of the sine wave (please have a look at the special point 4), the relative phase related to the sector origin, the absolute phase in between 360 degrees and the resulting sine waves. The added values in the right row (int) give an impression of the  integral = energy of the curve. The curves represent the 4 used points. The blue curve represents the angle from 0 ... 90 degrees.

Advantage of the method 2

Bei Nutzung der Methode 2 ergibt sich der Vorteil, dass sich gerade bei kleinen Tabellen eine etwas größere Amplitude unterbringen lässt, da bei gerader Punktanzahl für die Viertelbogen immer Symmetrie zur Zeitachse herrscht. Die Werte liegen also z.B. bei 4 Bit nicht bei 7,6,5 ... -5,-6,-7 unter Verlust des Punktes "-8", der ja möglich wäre, sondern bei 7,5 ... -7.5, womit alle 16 Punkte genutz werden können und die Welle trotzdem symmetrisch zu 0 bleibt. Ferner fällt der alleinige Maxwert weg, wodurch die Skalierung weiter wachsen kann (z.B. 32,1 im Bild), was besonders bei kleinen Auflösungen durchaus relevant ist. Nutzbar ist der Effekt immer dann besonders stark, wenn der Wert direkt auf einem Wandler ausgeben wird. [Bearbeiten] Mögliche Probleme Der Nachteil, dass es bei Methode 2 keinen ausdrücklichen Nullpunkt gibt, ist bei vielen Anwendungen unerheblich - wäre aber im Einzelfall zu prüfen, z.B. wenn ein Motor direkt durch Phase=0 abgeschaltet werden soll und eine echte "0" am Wandlerausgang benötigt wird. Grundsätzlich muß auch bedacht werden, daß im Falle einer Nachbehandlung der Sinuswellen durch interne digitale Filter generell größere Werte entstehen können, als durch die Stützstellen vorgegeben wurden, was bei größeren Amplituden ein Problem wird. Sicherheitshalber verzichtet man auf die Amplitudenüberhöhung und reduziert diese sogar, z.B. im Hinblick auf Fehlerreduktion, wie oben beschrieben. [Bearbeiten] Vergleich und Fazit In der Regel ist Definition 2 vorzuziehen. Bei großen Auflösungen nähern sich beide ohnehin an, es bleibt aber der Vorteil der einfacheren Behandlung der Vektoren und es gibt keine Sonderbehandlung des 90°-Falles. Hier bräuchte man je nach Realisierung eine Fallunterscheidung oder ein Bit mehr für die Vollaussteuerung. Gleiches gilt bei der Bildung der Phase.

Analytical calculation the the sine values

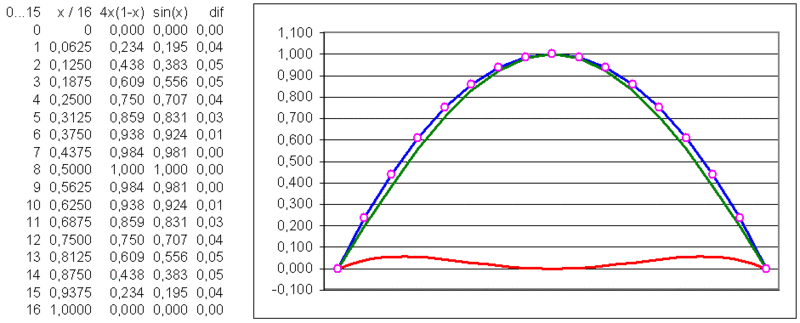
sche Annäherung Die Sinuswelle kann durch einen Parabelbogen angenähert werden, wenn eine schnelle Multiplikation zur Verfügung steht: [Bearbeiten] Sinus-Approximation 1 sin(π·x) und Approximation zweiter Ordnung im Intervall [0,1]Die nachfolgende Formel beschreibt dagegen eine einfache Approximation: Der Faktor 4 ist so gewählt, daß der Scheitel der Parabel mit dem Maximum der sin-Kurve zusammenfällt. Die Abweichung dieses leicht oberhalb des Sinus verlaufenden Bogens beträgt nicht mehr als 12.5%[1] und eignet sich daher für viele Applikationen, bei denen es nicht auf 100% Genauigkeit ankommt, oder die Abweichung akzeptabel ist. -------------------------------------------------------------------------------- [Bearbeiten]

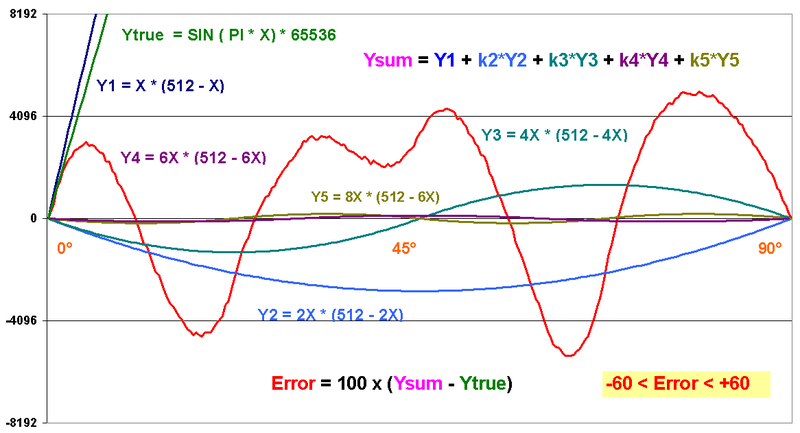
Sinus-Approximation 2 Durch Anwendung von Korrekturwerten, die aus Vielfachen der anregenden Frequenz gewonnen werden, können die Oberwellen im Endwert reduziert werden. Der Definitionsbereich wird dabei einfach durch Multiplikation des Einspeisevektors mit einem größeren Faktor abgetastet, wobei ab den Oberwellen 4 und folgende der resultierende Y-Wert zwischen zwei Nulldurchgängen manuell invertiert werden muss, um den jeweils inversen Halbbogen zu bilden. In C kann das durch die Signum/ABS-Funktionen erfolgen, in VHDL durch Nutzung des jeweiligen entstehenden MSBs. Die resultierenden Funktionen für die Oberwellen Y2 ... Y5 werden mit geeigneten Korrekturfaktoren multipliziert und addiert, sodass sich die Fehler minimieren. Funktionen und Fehler (rot, 100-fach gezoomed) bei Approximation fünfter Ordnung im Bereich 0...90°.Im obigen Beispiel wurde für die Abbildung des benötigten Sinus-Viertels ein 8Bit-Vektor (0...255) angenommen und 4 Oberwellen herangezogen. Die Phase wird daher auf 10Bit => 1/1024 genau abgebildet. Die Koeffizienten lauten: k1 = 1,0000, k2= -0,0444, k3= -0,0207, k4= -0,0018, k5= -0,00255. Die Abweichung des Ausgangswertes vom idealen Sinus (grün) beträgt hier ca. +/-45 digit pro Vollaussteuerung (hier 65536), was bewirkt, dass man mit der obenstehenden Vorschrift durch Weglassen der unteren 5 Bits einen Endwert mit +/- 1 digit Fehler (~ 0,1% Genauigkeit) erzielen kann, was gut zur gewählten Phasenauflösung passt. Eine in VHDL realisierte Schaltung läuft in einem Altera Cyclone FPGA rein kombinatorisch mit nahezu 50MHz. -------------------------------------------------------------------------------- [Bearbeiten]

Weiterverarbeitung

 Bei der direkten Erzeugung des Wertes durch Formeln kann die Berechung mit jeder beliebigen Auflösung erfolgen. Eine Interpolation oder Filterung ist in diesen Fällen nicht unbedingt nötig. Um dennoch Zwischenwerte zu bekommen gibt, es folgende Möglichkeiten: [Bearbeiten] Interpolation Die bisher nicht genutzten unteren Bits des Phasenakkumulators werden in eine Geradengleichung eingesetzt, wobei die Steigung und der Achsenabschnitt aus dem aktuellen und dem nächsten Punkt gewonnen werden. Wird eine Tabelle benutzt und neben dem Sinus auch der Cosinus erzeugt, so gibt die jeweils andere Funktion bereits die Steigung an und kann mitverwendet werden. Für schnelle Applikationen lohnt sich in jedem Fall die ausdrückliche Hinterlegung der Steigung. Durch die Nutzung einer Interpolation werden die Artefakte infolge der begrenzten Tabellengrösse stark gemindert. [Bearbeiten]

 Filterung

Eine anschliessende Filterung kann die Güte des Sinus weiter erhöhen. Ein einfaches, auf die zu erzeugende Frequenz abgestimmtes, IIR-Filter dämpft zuverlässig die hochfrequenten Anteile, also die verbleibenden "Knicke" der Interpolation. Die einfachste Implementierung ist ein Filter mit binären Koeffizienten vom Typ: Y(t+1) = Y(t) - Y(t)/k + SinusWert/k, wobei k = 16,32,64 ...! Eine Filterung ist insbesondere dann vorteilhaft, wenn ein Umsteuern der Frequenz erfolgt und Phasensprünge geglättet werden sollen. [Bearbeiten]

Dithering

Anwendungsbeispiele

Signalsynthese [Bearbeiten] Tongeneration In den 80ern konnte ich (in Assembler!) so ohne Interpolation oder Filterung wie bei einer DDS arbeiten und mit dem VC20 und VC64 Pseudo-Sinustöne erzeugen, die in der Frequenz genau zu variieren waren. Bei nur ca. 2MHz Taktfrequenz liessen sich mit einer einfachen Schleife schon bei 64 Punkten Sweeps und kontinuierliche Portamentoeffekte für das komplette Audiospektrum mehrkanalig produzieren. Die im Signal freilich enthaltenen Oberwellen wirken dabei mit zusätzlicher Musikalität :-) [Bearbeiten] Motorsteuerung Bei dem Betrieb von Schrittmotoren werden die X/Y-Wicklungen mit Strömen angesteuert, die Sinus/Cosinus-Verläufe aufweisen, um einen Feinschrittbetrieb zu ermöglichen. Die im Signal enthaltenen Oberwellen sind hier sogar günstig für den Beschleunigungsverlauf, da die Steigungen der Funktion genau dort grösser sind, als der echte Sinus, wo der Motor aufgrund des Haltemoments am meisten Widerstand entgegen setzt. (Nur ein Motor ohne Haltemomentpunkte würde 100%ige COS/SIN benötigen). [Bearbeiten] Signalverarbeitung [Bearbeiten] Fensterung Durch partielle Nutzung der Halbbögen der Sinusapproximation 1 kann in einfacher Weise eine effektive Fensterfunktion für Filter und FFTs erzeugt werden. [Bearbeiten] IQ-Modulation Der Vorteil der kontinuierlichen, nicht an Tabellen gebundenen, Sinussynthese zeigt sich besonders bei der IQ-Modulation, wo die Akkumulatorrundung bei kleinen Tabellen ohne eine Interpolation zu weiterem unerwünschtem Phasenrauschen führt, das minunter schwerwiegendere Fehler generiert, als der systematische Amplitudenfehler. Allerdings ist zumindest Annäherung 2 zu verwenden.