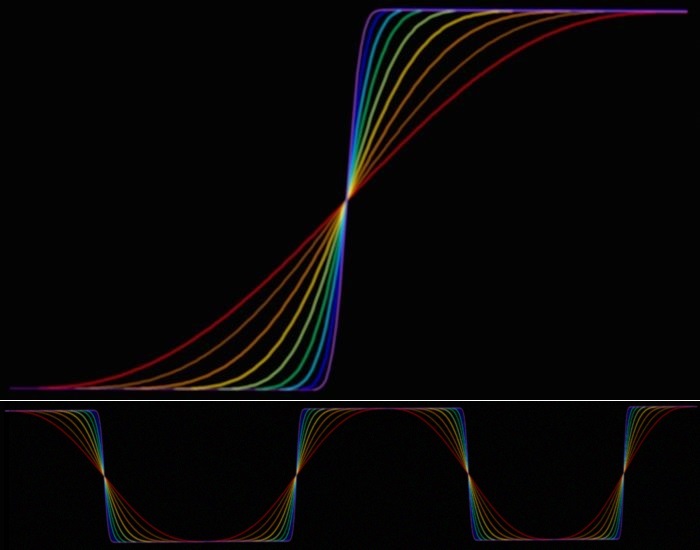
This page shows functions with programable saturation behavior based on polynoms. They can be used for smoothing operations, cross fading in between two channels but also wave generation by edge shaping, which can be used to limit and also generate harmonics.

wave generation with saturation functions  

The slope of the curves and the degree of saturation can be easily adjusted, allowing the harmonics of the curve to be specifically limited. In this way, square waves can be synthesized from scratch with a well defined bandwidth limit. The calculation is performed by an iterative procedure - specifically, by continued multiplication followed by numerical integration. Alternatively, the full formula can also be rolled out in order to then integrate it. The implementation depends on the particular usage of your DSP.

The functions are derived from the equation Y = 4 * X * (1-X) which leads to a parabolic arc at first. This function is squared several times to obtain bell curves with a decreasing width which then are integrated. The range for X is 0 ... 1. The factor 4 is to scale it that way that it reaches the 100% at the top of the curve. The integrated functions are scaled in a simular way to end up at 100%. Prime number splitting is used for this.

First stage Y1 = 4 * ( x - x*x)  = 4 * (x-x2)
Integral (Y)  =  3/2 * 4 * (X*X/2 - X*X*X / 3)  -> 3*X*X - 2*X*X*X
Simpified scaled Integral to cover 0 ... 1: Y = 3x2 - 2x3  for x = 0 ... 1

Second stage: Y2 = Y1*Y1  =  16 * ( X*X - 2*X*X*X + X*X*X*X )
Integral (Y1*Y1) = 16 * (X*X*X / 3 - X*X*X*X / 2  + X*X*X*X*X / 5) = 1/3*x3 - 1/4*x4 ....
to be able to use it, it shall be scaled by ratio 2*3*5 = 30 leading to:
Simplified scaled Integral to cover 0 ... 1:  10*x3 - 15*x4 +6*x5

Third stage: Y3 = Y1*Y2
this stage is unused because we want even harmonics in musics

Forth stage: Y4 = Y2*Y2  =  ...
must be scaled with 2*3*5*7*3 / 16 / 16
Simplified scaled Integral to cover 0 ... 1:  126*x5 - 420*x6 + 540*x7 - 315*x8 + 70*x9
The simplified equation is more appropriate for INT-calculation in DSPs, because finally there is a division by 2,4,8 ... only.

Fith stage = Y1*Y4 = Y2*Y3
unused here because of odd harmonics

Forth stage: Y6 = Y3*Y3  =  ...
x8 - 8x9 + 28x10 - 56x11 + 70x12 - 56x13 + 28x14 - 8x15 + x16
Integral = x9 /9 - 8x10 / 10 + 28x11 / 11 - 56x12 / 12 + 70x13 / 13 - 56x14 / 14 + 28x15 / 15 - 8x16 / 16 + x17 / 17
must be scaled with 2*3*13*15*17 / 256 / 256 = 218700 / 65536
= 24310*x9 + 175032*x8 .....  12870*x17

the full rolled out calculation becomes ineffective from here so only sequentially squaring makes sense.

A complete model with parameterization is available as C code.

Download C-App for Chameleon DSP: Parametric Saturation Distorsion