| 96 kHz.org |
| Advanced Audio Recording |
|
Comparison between 48kHz, 192kHz and 768kHz sample frequency In another article some technical background was shown, why higher sample rates give us significant advantages for recording and audio signal processing. Please refer to these articles Advantage of 192kHz and Comparison 48/96/192/384kHz. Regarding recording situations, 192kHz appears totally sufficient to maintain the quality available from the typical analog equipment like consoles and microphones while 96kHz appears to be sufficient for sound reproduction. In most cases 192kHz should also be nice for sound synthesis but in this article, I like to give you an idea why and when 768kHz might be required to synthesize signals appropriately: The advantage of high oversampling From the theory 48kHz frequency seem to be sufficient to represent up to 24kHz waves meeting nyquist's criteria. Regarding the issue of appropriate reconstruction filters a moderate oversampling of ratio 2 or 4 should be enough to deal with all frequencies in the audio spectrum. But if we have a look at extreme sound synthesis cases, higher frequencies might occur which will cause unwanted effects leading to the conclusion that 768kHz should be chosen in some cases. This is interesting since for sound synthesis 192kHz is the currently preferred frequency and 384kHz is currently the highest discussed frequency for audio signal representation in Software-DAWs.
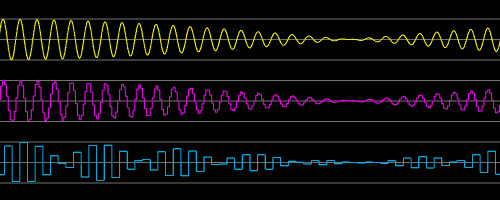
To understand the issue let's have a look at classical analog synthesis using square wave and phasing. A square wave derived from an oscillator and a comparator circuit will create an impulse with an infinite steepness which is practically limited to some MHz because of the bandwidth of the circuit components. At first sight this signal can be represented with digital samples easily as long as nyquist is fulfilled. The first problem is, that both starting point and end point of time of the square are not perfectly ideal because of phase granularity which will cause jitter. As long as this wave is working alone this might be non audible. But a second issue now is phasing, that means mixing this pulse with another pulse created the similar way: A phasing effect in the analog domain will be achieved that way that a second wave is introduced having the same amplitude and a slightly differing phase. This will cause any possible phase constellation between the two waves and lead to all cases in between summation to the double of the amplitude and total subtraction to zero. To optically analyze various possibilities in one diagram a slightly different frequency is used to cover different cases in one simulation: The subsequent image shows three cases of two sine wave at 21400Hz and 21900Hz individually sampled at 48kHz (cyan), 192kHz (purple) and 768kHz (yellow). They are then digitally mixed together at one bus. Although we are dealing with already lightly super sonic waves here, there seems to be no problem, using 48kHz only to represent them correctly assuming an appropriate AA-filter to reconstruct the waves finally. There is only a kind of amplitude modulation which is caused by the initial sampling of the wave, but a) this is a normal behavior of the filter and b) will be removed since the frequency will be beyond the edge frequency. Even if parts of this signal remain in the final analog signal at the output however, it will be a frequency which hardly will be represented in the loudspeakers and if so, it will be inaudible. So we can assume no issue here at all and can point out that 48kHz will be fine for all other mixing products of sine frequencies below 20kHz.
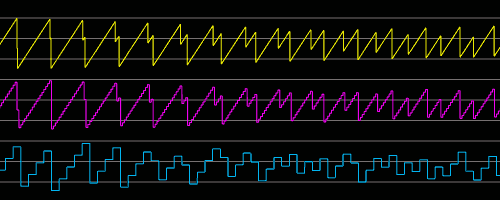
As the next image shows, this is different with the other classical waves like saw tooth and triangle. In the example below saw tooth waves of "only" 5400Hz and 5650Hz are sampled and then again mixed together. The yellow (768kHz) digital signal seems to show the mixing pretty well and comes close to the result which we had had using an analog synth. The well known sound effect of frequency sliding / doubling occurs. Also in the 192kHz curve it seems to be represented correctly, whereby a detailed look shows, that there are already little issues. The 48kHz curve is pretty bad, and does not represent the signal at all. It is far way from that what we had expected from a mixing result in the analog domain, since a large part of the harmonic frequencies of the triangle cannot be represented by 48kHz generally.
Moreover the cyan signal shows up with frequencies lower than the base frequencies used for mixing and contains strong spectral artifacts. The result is that the reconstructed signal after the filter will have audible parts! This is not appropriate at all since those parts of the spectrum would have caused supersonic waves in the analog domain which would not be inaudible. The result is a harsh and crispy additive to the sound instead of a smoothed sound. This will show up with chords strongly. And this issue can become even worse, as the following image shows:
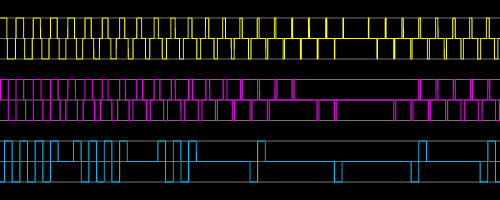
Here two perfect squares at 21400Hz and 21900Hz were mixed together in their particular sampling frequency domain. Regarding this example the total spectrum of the mixture should not be in the audible range at all since the base waves aren't. In the analog domain this would be perfectly fulfilled. But in the digital domain the result is not as expected:
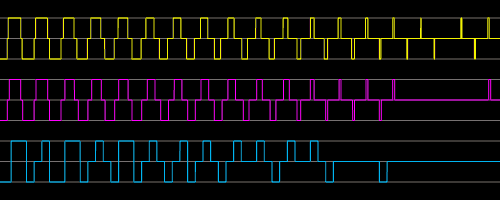
Only the 768kHz domain shows a very little artifact in representing the very small pulses. Detailed investigation shows, that this is also the case for other constellations of frequencies and the resulting phase offsets. The two waves having either +1 or -1 perfectly add to either -2, 0 or -2. There is a pretty smoothed and continuous behavior over the sweep representing also very small pulses close to case when ideal wave cancelling takes places because the signals temporarily are the same. Filtering this signal will lead to silence in the audible range as expected. So we can point out that the non audible frequencies in a square wave cause no mixing products which show up the wrong way later. The reason is, that the amount of energy of the harmonics beyond the audible frequency limit is mostly covered by those frequencies which are still below the nyquist frequency of 384kHz. The Fourier analysis of e.g. a 20kHz square signal gives a level of (1/19)2 for 380kHz. The issues are also still acceptable with 192kHz, except that in some extreme case low frequency components are introduced. With 48kHz this is really ugly: Neither there is a continuous behavior regarding phasing nor are all frequencies maintained in the inaudible range. In the opposite: This signal will cause a strong distorted and non harmonic sound while it's analog competitor would not create this at all. This is also evident in the more practical case with lower frequencies which are still audible like 13400Hz and 13800Hz which is shown in the next image:
For the 48kHz case (cyan) after the anti aliasing filter at the output, the final signal in the analog domain will contain relevant components of audible frequencies which are newly introduced - just because the sound generation has been done the digital way although nyquist's criteria has been considered to be respected corrcetly. In fact it was not because it was not an ideal sine wave. Now, what is the conclusion? How far do we have to go? According to the typical bandwidth in analog audio systems, which can be assumed to be around 50kHz and below, we usually do not need to estimate a higher bandwidth for sound synthesis either. Even for triangles and squares we can consider them to be band limited in analog synthesizers too. So representing e.g. 150kHz appropriately should be the target to go for. Band limiting a square wave or triangle down to 150kHz is the key to operate them correctly especially when mixing them together in the digital domain. Using oversampling of a ratio 4 to 8 should be enough to represent the waves themselves leading to 400 ... 800kHz for the sampling frequency. Practical experiments with super sonic wave synthesis and processing them proved that in real. There was no difference anymore between analog and digital waves when operating the band limiting correctly.
|
| © 2006 J.S. |